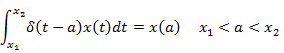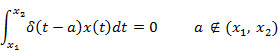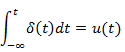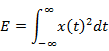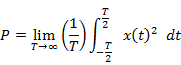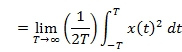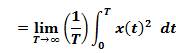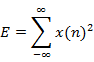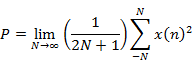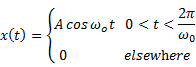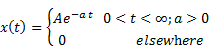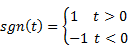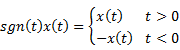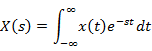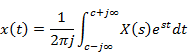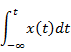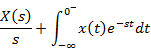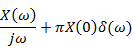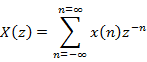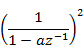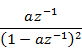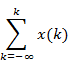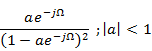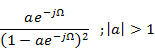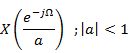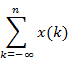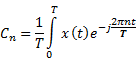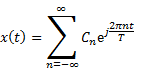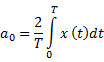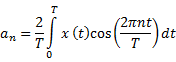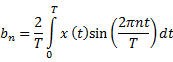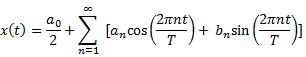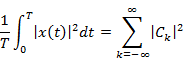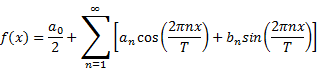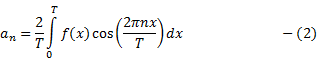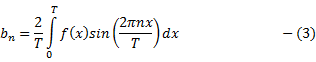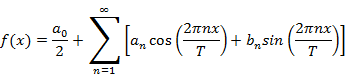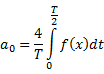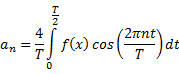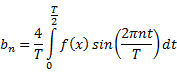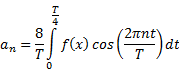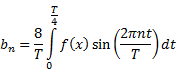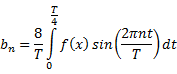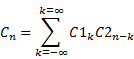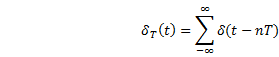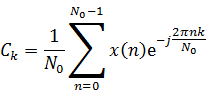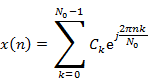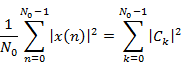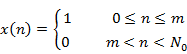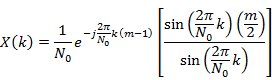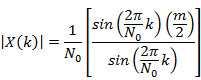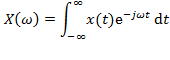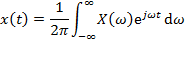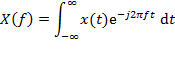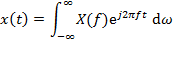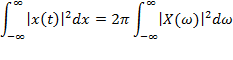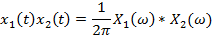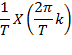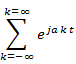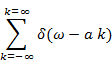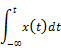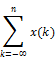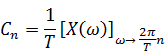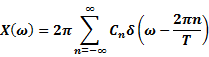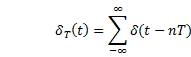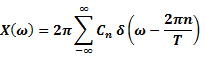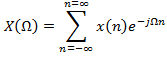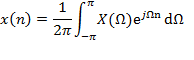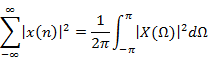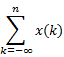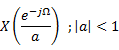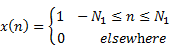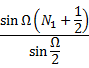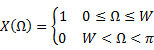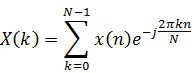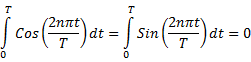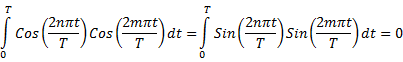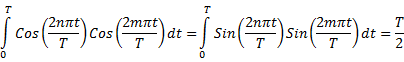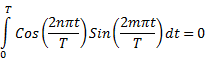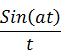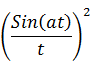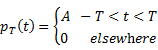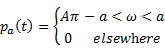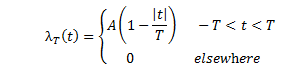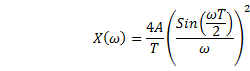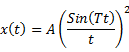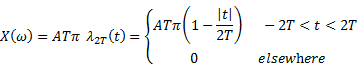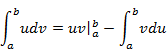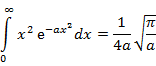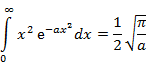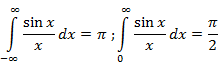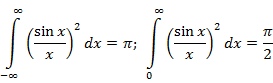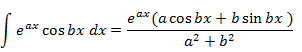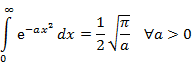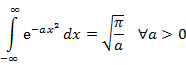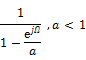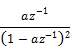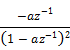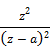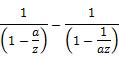Contents

SIGNAL BASICS. 1

Signal properties. 1

Impulse signal 1

Energy & Power. 2

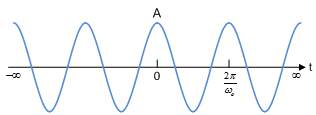
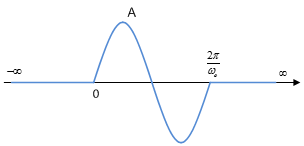
Examples of Energy and Power Signals. 2

Even & Odd Decomposition. 3

Complex COnjugate Symmetry. 3

LTI SYSTEMS. 4

Signum Functions. 5

Sinusoidal fucntions. 5

Laplace Transform.. 5

TablE-1 of Laplace Transform.. 5

Table-2 of Laplace Transform.. 6

Partial fraction. 7

Z Transform.. 8

Table-1 of Z-Transforms. 8

Z-Transform and DTFT. 9

SYstem properties of Z-Transform.. 10

jury’s Table Stability Test 10

Fourier-Analysis. 11

Continuous Time Fourier Series. 11

Relationship between  and its CTFS coefficients. 11

Properties of . 12

Drichilet’s Condition. 12

HALF WAVE SYMMETRY. 13

CTFS- Table. 14

Examples 0f CTFS. 14

Discrete-Time Fourier Transform.. 15

Discrete time Fourier series coefficients of a periodic signal  with period . 15

Relationship between  and . 15

Properties of . 16

Comparison between coefficients of CTFS & DTFS. 16

Relation between CTFS & DTFT. 16

DTFS TABLE. 16

Continuous-time Fourier transform.. 17

Relationship between  and .. 17

Properties of . 18

Comparison between coefficients of CTFT & DTFS. 18

CTFT VS LAPLACE. 18

CTFT Vs DTFT. 19

Examples CTFT. 20

Discrete Time Fourier Transform.. 21

Discrete-time Fourier transform.. 21

Relationship between  and .. 22

Properties of . 22

DTFT Table. 22

Discrete Fourier Transform.. 23

Trigonometry for Fourier Analysis. 24

Examples. 24

Introduction of Hilbert Transform.. 25

SINC FUNCTION.. 25

Rectangular Function. 26

Triangular Function. 27

Important Integrals. 28

TABLE. 29

SIGNAL BASICS

Signal properties

	First flip  and then apply time shift
	First apply time shift and then flip  about

Impulse signal

Scaling property		Important property it is used in Fourier Transforms for replacing function  with.
Integration property
Even function
Relation with step function
Relation with signum function
Relation with arbitrary function

Energy & Power

Energy of a signal		is called normalized energy in the signal
Power of a signal		is called normalized average power in the signal
Energy of a signal		is called normalized energy in the signal
Power of a signal		is called normalized average power in the signal

 is called an energy signal if its Energy  satisfies the condition

 is called a power signal if its Power  satisfies the condition

· Power signals have finite average power and infinite energy.

· Energy signals have finite energy and zero average power.

Examples of Energy and Power Signals

Signal		Power	Energy
		0
		0

Even & Odd Decomposition

Any signal  can be represented by sum of an its even and odd function.

Complex COnjugate Symmetry

If  Z(x)=A(x)+jB(x)  is Complex Conjugate Symmetric then

Example :   is CCS

 is  CCAS

 is neither CCS nor CCAS

If  Z(x)=A(x)+jB(x)  is Complex Conjugate Anti-Symmetric then

CCS	CCAS

LTI SYSTEMS

A system  is said to be linear if it satisfies the following two conditions:

1.

2.

A system  is said to bet time-invariant if it satisfies the condition:

1.

Examples:

Linear Systems	Non Linear Systems

Time Invariant System	Time Variant System

Response to LTI Transfer Functions

Signum Functions

1.

2.

Sinusoidal fucntions

Signal	Period
	Not periodic

Laplace Transform

Laplace Transform

Inverse Laplace Transform c is selected in such a way that if  then

TablE-1 of Laplace Transform

Signal	Laplace Transform	Fourier Transform	Remarks
1			Duality Theorem
	1	1
			Special Type

Signal	Laplace Transform	Fourier Transform

Signal	Laplace Transform	Fourier Transform

Table-2 of Laplace Transform

Partial fraction

Z Transform

Z Transform

Inverse Z Transform

Table-1 of Z-Transforms

		ROC : all z
		ROC :
		ROC :
		ROC :
		ROC :    where ROC : Does not exist if
		ROC :
		ROC :
		ROC :
		ROC :
		ROC :
		ROC :
		ROC : 1/
		ROC :
		ROC :
		ROC :
		ROC :

Z-Transform and DTFT

Signal	Z-Transform	DTFT
			ROC : all z
			ROC :
			ROC :
			ROC :
			ROC :    where ROC : Does not exist if
			ROC :
			ROC :
			ROC :
			ROC :
			ROC :
			ROC :
			ROC : 1/
			ROC :
			ROC :
			ROC :
			ROC :

SYstem properties of Z-Transform

STABILITY	A system is stable if	ROC contains the unit circle.
CAUSALITY	A system is causal if	This means that ROC will start at the pole with largest magnitude and would extend to infinity
ANTICAUSALITY	A system is anticausal if	This means that ROC will start at the pole with smallest magnitude and would extend towards origin.
STABILITY  AND CAUSALITY	Stable and causal means	ROC should contain the unit circle and starts from the largest pole and extends outwards.  This implies that all the poles of such a system should be within the unit circle OR the magnitude of all the poles should be less than unity.

jury’s Table Stability Test

Stability of System:

The denominator of Transfer function polynomial is called the characteristic equation. It should satisfy the following necessary but not sufficient condition.

a.

b.

If conditions (a) and (b) are satisfied then D (z) is tested using JURY’S TABLE.

Row
1				.….
2				.….
3				.….
4				.….
5				.….
6				.….
: :	: :	: :	: :	: :	: :

a. First row is prepared in the ascending order of z.

b. Second row is prepared by substituting the coefficients of first row in reverse.

c. Third row coefficients are calculated as : =

d. Fourth row is prepared by substituting the coefficients of third row in reverse.

e. Fifth row coefficients are calculated as :  =

f. This process is continued till  row with the last element

g. Now apply JURY'S TEST. As per  the test the following condition are to be satisfied

…

..

Fourier-Analysis

Continuous Time Fourier Series

Continuous time Fourier series coefficients of a periodic signal  with period

Complex Form
Trigonometric Form
Harmonic Form
Relationship between complex, trigonometric and harmonic form		n≠0
Power in  expressed in terms of Fourier coefficients		(Single-Sided   Spectrum)            (Double-Sided Spectrum)

Relationship between 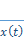 and its CTFS coefficients

Real + Even	Real + Even
Real + Odd	Img + Odd
Img + Even	Img + Even
Img + Odd	Real + Odd
Real	Complex Conjugate Symmetric
Img	Complex Conjugate           Anti-symmetric
Even	Even
Odd	Odd
Complex	Complex
Complex Conjugate Symmetric	Real
Complex Conjugate Anti Symmetric	Imaginary

Properties of

Periodicity	is aperiodic
Duality	No duality
Conjugation
Real and odd parts
Parseval's Theorem
Multiplication
Convolution

Drichilet’s Condition

Suppose that a function  is such that :

1.  is periodic with period

2.  is defined and single-valued except possibly at a finite number of points in .

3.  and  are piecewise continuous in

then  can be represented by a series called Fourier series given as

· The Fourier series converges to  if  is a point of continuity.

· At point of discontinuity it converges to the value

HALF WAVE SYMMETRY

Even Function
Odd Function
Half-Wave Symmetric (HWS)
HWS and even
HWS and odd

CTFS- Table

1
	]
	]
]
]

Examples 0f CTFS

Signal	Fourier Coefficients
is periodic with period =
and  are both periodic with period   and fourier coefficients  and . If   is another signal such that  and is also periodic with period  and fourier coefficients  then fourier coefficients of  can be obtained from that of  and

Discrete-Time Fourier Transform

Discrete time Fourier series coefficients 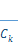of a periodic signal  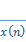with period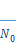

 is called digital frequency.

Relationship between  and

Real + Even	Real + Even
Real + Odd	Img + Odd
Img + Even	Img + Even
Img + Odd	Real + Odd
Real	Complex Conjugate Symmetric
Img	Complex Conjugate Anti-symmetric
Even	Even
Odd	Odd

Properties of

Periodicity
Duality
Conjugation
Real and odd parts
Parseval's Theorem

Comparison between coefficients of CTFS & DTFS

n varies from  to
Aperiodic	Periodic

Relation between CTFS & DTFT

DTFS TABLE

1
	]
	]
]
]
	Phase

Continuous-time Fourier transform

· Drichlet's Condition:  should satisfy the given conditions to have Fourier-Transform

·

· should have finite number of maxima or minima in a finite interval.

· should have finite number of finite discontinuities in any finite interval.

· Relationship between CTFT and LT

· Find LT of the given signal.

· Substitute

· The result is FT.(Click for example). [Note: if the signal is not absolutely integrable then this method does not work.(Click for example)]

Relationship between  and

Real + Even	Real + Even
Real + Odd	Img + Odd
Img + Even	Img + Even
Img + Odd	Real + Odd
Real	Complex Conjugate Symmetric
Img	Complex Conjugate Anti-symmetric
Even	Even
Odd	Odd

Properties of

Periodicity	is aperioidic
Duality
Conjugation
Real and odd parts
Parseval's Theorem
Group Delay
Convolution
Multiplication

Comparison between coefficients of CTFT & DTFS

Periodic	Aperiodic

CTFT VS LAPLACE

Signal	Fourier Transform	Laplace Transform
1
	1	1

CTFT Vs DTFT

Signal	CTFT	Signal	DTFT
1		1
	1		1

Examples CTFT

Problems	Solution
Any signal  when convoluted with  gives the signal back.
Given the signal  and its Fourier transform . Find the Fourier coefficient of a signal  obtained by repeating  and has a period .
Fourier Transform of a periodic signal  with period  and Fourier series coefficients
Fourier Transform of a periodic impulse train

Discrete Time Fourier Transform

Discrete-time Fourier transform

· Drichlet's Condition:  should satisfy the given conditions to have Fourier-Transform

·

· should have finite number of maxima or minima in a finite interval.

· hould have finite number of finite discontinuities in any finite interval.

· Relationship between CTFT and LT

· Find LT of the given signal.

· Substitute

The result is FT.(Click for example). [Note: if the signal is not absolutely integrable then this method does not work.(Click for example)]

Relationship between  and

Real + Even	Real + Even
Real + Odd	Img + Odd
Img + Even	Img + Even
Img + Odd	Real + Odd
Real	Complex Conjugate Symmetric
Img	Complex Conjugate Anti-symmetric
Even	Even
Odd	Odd

Properties of

Periodicity	perioidic
Duality	Does not exist
Conjugation
Real and odd parts
Parseval's Theorem
Convolution
Multiplication

DTFT Table

Signal	DTFT
1	2π δ(Ω)
	1

Discrete Fourier Transform

DFT is discrete Fourier Transform is a modification of  FT-Discrete Time.

· FT-Discrete Time is continuous in  with period 2.

· This continuous function is made discrete for computational efficiency and is known as DFT

DFT:

·  is not periodic but zero outside

·  is periodic with period

·  is called the Twiddle Factor

·  is the Twiddle Notation

· Calculation of   involves

·  addition

·  multiplication

Trigonometry for Fourier Analysis

Note: The generic form for all the relations is that if the time period is  then

Examples

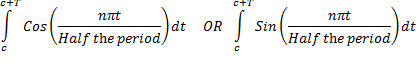
1. A  periodic signal , with fundamental frequency   is sampled at a  frequency giving a periodic discrete-time signal with fundamental period . What is the relationship between  and  ?

Ans:  where  and  is a positive integer

2. A signal  is periodic with fundamental frequency . What is the relationship between  and  ?     

Ans:  where  and  is a positive integer. 

Introduction of Hilbert Transform

HT of a signal  is defined as 

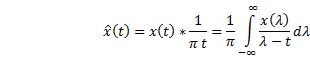
1. Amplitude spectrum of  and  is same.

2.  and  are orthogonal.

3.

4.

Signal	Fourier Transform

SINC FUNCTION

There are two definitions of   namely  : 1)Mathematics:        2)  Engineering:

Time Signal	Fourier Transform

Rectangular Function

A rectangular function of time is defined as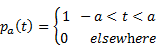

Time period of  is

Signal	Fourier Transform

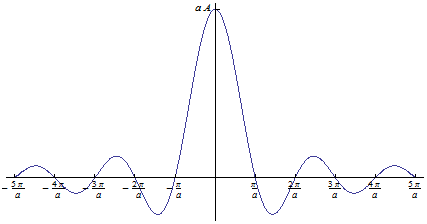
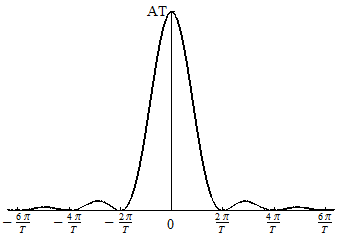
· This is an important transform pair and it finds application in many problems of signals and systems.

· The frequencies are in . So in terms of  there will be a factor .

Triangular Function

Important Integrals

TABLE

PROPERTY	SIGNAL	Z-TRANSFORM	Discrete-Time FT	ROC
Impulse		1	1	all z except z=0 and z=∞
Right-shifted-Impulse				all z except at z=0
Left-shifted-Impulse				all z except at z=∞
Unit Step
Reverse Unit Step(special)
Reverse Unit Step
Ramp
Reverse Ramp
Reverse-Ramp-Special
Time-Multiplication
Time-Multiplication Time reversal
Time-Multiplication Time reversal
Modulus Time				ROC exists only if |a| < 1. ROC does not exist if |a| > 1.
Time Reversal				ROC'=1/ROC( Take the reciprocal of the magnitude and inverse the region, the inequality also gets reversed).
Exponential Multiplication				ROC remains the same.
Multiplication				ROC'=|a| ROC. Amplification of the region of convergence.
Differentiation in Time				ROC remains the same.
Accumulation in Time				ROC'= ROC ∩{|z|>1}
INITIAL VALUE Theorem
FINAL VALUE Theorem
PERIODIC Signal in time
STABILITY		A system is stable if		ROC contains the unit circle.
CAUSALITY		A system is causal if		This means that ROC will start at the pole with largest magnitude and would extend to infinity
ANTICAUSALITY		A system is anticausal if		This means that ROC will start at the pole with smallest magnitude and would extend towards origin.
STABILITY AND CAUSALITY		Stable and causal means		ROC should contain the unit circle and starts from the largest pole and extends outwards.  This implies that all the poles of such a system should be within the unit circle OR the magnitude of all the poles should be less than unity.